How Do You Know When You Use Iqr or Standard Deviation
Variability describes how far apart information points lie from each other and from the centre of a distribution. Along with measures of central trend, measures of variability give you descriptive statistics that summarize your data.
Variability is also referred to every bit spread, scatter or dispersion. Information technology is almost commonly measured with the following:
- Range: the departure between the highest and lowest values
- Interquartile range: the range of the heart one-half of a distribution
- Standard deviation: average altitude from the hateful
- Variance: average of squared distances from the hateful
Why does variability matter?
While the cardinal tendency, or average, tells you where most of your points lie, variability summarizes how far apart they are. This is important because the amount of variability determines how well you tin generalize results from the sample to your population.
Depression variability is ideal because information technology means that you tin can better predict information about the population based on sample data. High variability ways that the values are less consistent, so information technology's harder to make predictions.
Data sets can accept the aforementioned cardinal trend but dissimilar levels of variability or vice versa. If you know only the key tendency or the variability, y'all can't say anything about the other attribute. Both of them together give you a complete picture of your data.
Using elementary random samples, you collect information from 3 groups:
- Sample A: loftier school students,
- Sample B: college students,
- Sample C: developed total-time employees.

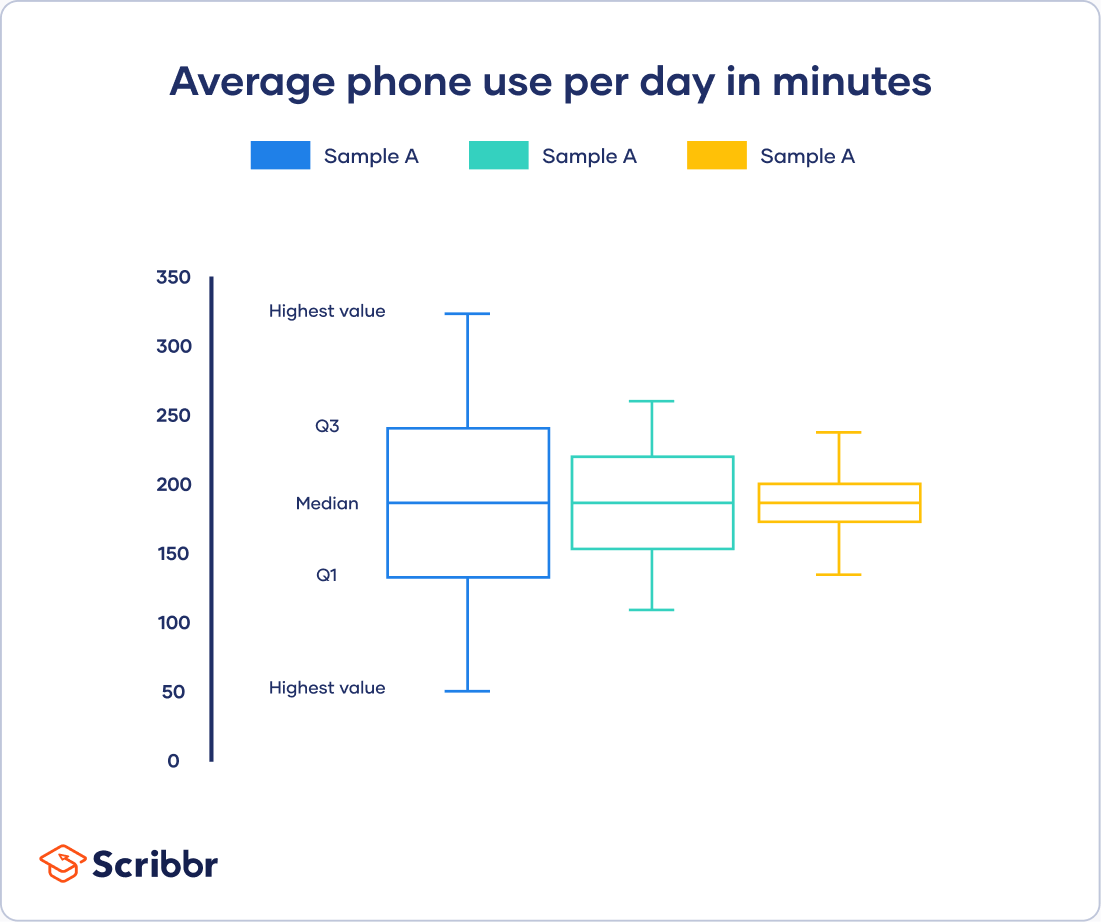
All three of your samples take the same average phone use, at 195 minutes or 3 hours and 15 minutes. This is the x-axis value where the acme of the curves are.
Although the data follows a normal distribution, each sample has different spreads. Sample A has the largest variability while Sample C has the smallest variability.
Range
The range tells yous the spread of your information from the everyman to the highest value in the distribution. It's the easiest mensurate of variability to calculate.
To find the range, simply subtract the lowest value from the highest value in the data set up.
| Data (minutes) | 72 | 110 | 134 | 190 | 238 | 287 | 305 | 324 |
|---|
The highest value (H) is 324 and the lowest (L) is 72.
R = H – L
R = 324 – 72 = 252
The range of your data is 252 minutes .
Because only 2 numbers are used, the range is influenced by outliers and doesn't give you lot whatsoever data virtually the distribution of values. It'southward all-time used in combination with other measures.
What is your plagiarism score?
Compare your paper with over threescore billion spider web pages and 30 1000000 publications.
- Best plagiarism checker of 2021
- Plagiarism study & percentage
- Largest plagiarism database
Scribbr Plagiarism Checker
Interquartile range
The interquartile range gives you the spread of the eye of your distribution.
For any distribution that'south ordered from low to high, the interquartile range contains one-half of the values. While the get-go quartile (Q1) contains the beginning 25% of values, the fourth quartile (Q4) contains the last 25% of values.
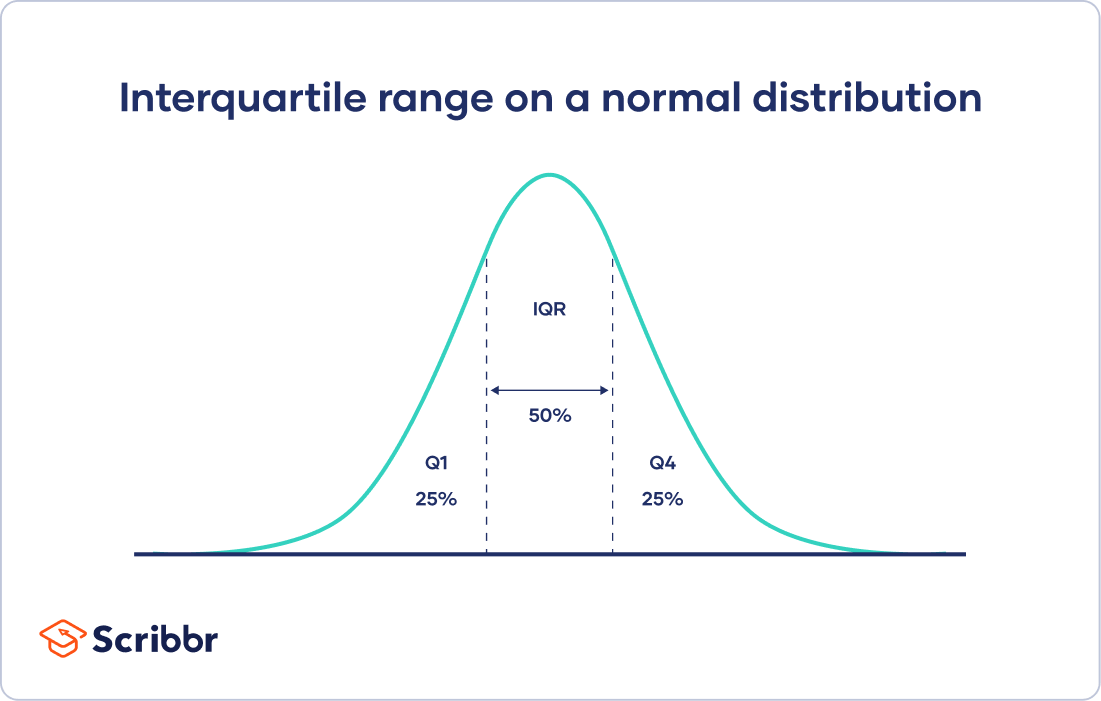
The interquartile range is the 3rd quartile (Q3) minus the first quartile (Q1). This gives u.s.a. the range of the middle half of a information set.
Multiply the number of values in the data set (eight) by 0.25 for the 25th percentile (Q1) and by 0.75 for the 75th percentile (Q3).
Q1 position: 0.25 x 8 = two
Q3 position: 0.75 x 8 = half-dozen
Q1 is the value in the 2nd position, which is 110. Q3 is the value in the 6th position, which is 287.
IQR = Q3 – Q1
IQR = 287 – 110 = 177
The interquartile range of your data is 177 minutes .
Just like the range, the interquartile range uses only 2 values in its calculation. But the IQR is less affected past outliers: the 2 values come from the middle half of the information prepare, and then they are unlikely to be extreme scores.
The IQR gives a consistent measure of variability for skewed too as normal distributions.
V-number summary
Every distribution can be organized using a five-number summary:
- Lowest value
- Q1: 25th percentile
- Q2: the median
- Q3: 75th percentile
- Highest value (Q4)
These five-number summaries can be easily visualized using box and whisker plots.
Standard deviation
The standard deviation is the boilerplate corporeality of variability in your dataset.
It tells you, on average, how far each score lies from the mean. The larger the standard deviation, the more variable the data set is.
There are six steps for finding the standard divergence by manus:
- List each score and find their mean.
- Subtract the hateful from each score to get the deviation from the mean.
- Square each of these deviations.
- Add upward all of the squared deviations.
- Divide the sum of the squared deviations by northward – ane (for a sample) or N (for a population).
- Detect the square root of the number yous found.
| Pace one: Data (minutes) | Pace 2: Deviation from hateful | Steps 3 + 4: Squared divergence |
|---|---|---|
| 72 | 72 – 207.5 = -135.5 | 18360.25 |
| 110 | 110 – 207.five = -97.5 | 9506.25 |
| 134 | 134 – 207.5 = -73.5 | 5402.25 |
| 190 | 190 – 207.five = -17.5 | 306.25 |
| 238 | 238 – 207.5 = 30.v | 930.25 |
| 287 | 287 – 207.5 = 79.5 | 6320.25 |
| 305 | 305 – 207.five = 97.five | 9506.25 |
| 324 | 324 – 207.five = 116.five | 13572.25 |
| Hateful = 207.5 | Sum = 0 | Sum of squares = 63904 |
n – 1 = seven
63904 / 7 = 9129.14
s = √9129.14 = 95.54
The standard deviation of your data is 95.54 . This means that on average, each score deviates from the hateful by 95.54 points.
Standard deviation formula for populations
If you have information from the unabridged population, utilize the population standard deviation formula:
| Formula | Explanation |
|---|---|
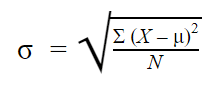 |
|
Standard deviation formula for samples
If y'all have data from a sample, use the sample standard deviation formula:
| Formula | Explanation |
|---|---|
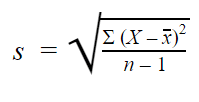 |
|
Why use north – 1 for sample standard divergence?
Samples are used to make statistical inferences about the population that they came from.
When you have population data, you lot can go an exact value for population standard deviation. Since you collect information from every population member, the standard deviation reflects the precise corporeality of variability in your distribution, the population.
Merely when yous apply sample data, your sample standard departure is always used every bit an estimate of the population standard difference. Using n in this formula tends to give you a biased judge that consistently underestimates variability.
Reducing the sample n to due north – ane makes the standard difference artificially large, giving you a conservative estimate of variability.
While this is non an unbiased guess, it is a less biased gauge of standard deviation: information technology is better to overestimate rather than underestimate variability in samples.
The difference between biased and conservative estimates of standard deviation gets much smaller when yous have a big sample size.
Variance
The variance is the boilerplate of squared deviations from the mean. A deviation from the mean is how far a score lies from the hateful.
Variance is the foursquare of the standard deviation. This means that the units of variance are much larger than those of a typical value of a information set.
While it's harder to interpret the variance number intuitively, information technology's important to calculate variance for comparing different data sets in statistical tests like ANOVAs.
Variance reflects the degree of spread in the information set. The more spread the information, the larger the variance is in relation to the hateful.
due south = 95.5
s 2 = 95.5 10 95.5 = 9129.14
The variance of your data is 9129.xiv.
To find the variance by hand, perform all of the steps for standard difference except for the final stride.
Variance formula for populations
| Formula | Explanation |
|---|---|
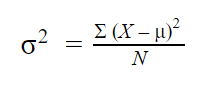 |
|
Variance formula for samples
| Formula | Explanation |
|---|---|
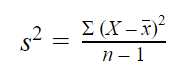 |
|
Biased versus unbiased estimates of variance
An unbiased estimate in statistics is ane that doesn't consistently give yous either loftier values or low values – information technology has no systematic bias.
Just like for standard deviation, in that location are different formulas for population and sample variance. But while there is no unbiased estimate for standard deviation, there is one for sample variance.
If the sample variance formula used the sample n, the sample variance would be biased towards lower numbers than expected. Reducing the sample n to n – ane makes the variance artificially larger.
In this instance, bias is not only lowered but totally removed. The sample variance formula gives completely unbiased estimates of variance.
So why isn't the sample standard deviation also an unbiased estimate?
That's considering sample standard deviation comes from finding the square root of sample variance. Since a square root isn't a linear functioning, like addition or subtraction, the unbiasedness of the sample variance formula isn't carried over the sample standard deviation formula.
What'south the best mensurate of variability?
The best measure of variability depends on your level of measurement and distribution.
Level of measurement
For data measured at an ordinal level, the range and interquartile range are the simply appropriate measures of variability.
For more complex interval and ratio levels, the standard difference and variance are also applicable.
Distribution
For normal distributions, all measures tin exist used. The standard departure and variance are preferred considering they take your whole data ready into account, but this too means that they are hands influenced past outliers.
For skewed distributions or data sets with outliers, the interquartile range is the best measure out. It's least affected by farthermost values because it focuses on the spread in the centre of the data prepare.
Oftentimes asked questions about variability
- What is variability?
-
Variability tells you how far apart points lie from each other and from the eye of a distribution or a data set.
Variability is also referred to as spread, scatter or dispersion.
How Do You Know When You Use Iqr or Standard Deviation
Source: https://www.scribbr.com/statistics/variability/
0 Response to "How Do You Know When You Use Iqr or Standard Deviation"
Post a Comment